ข้อมูลเศรษฐกิจที่มีความถี่ต่างกัน…วิเคราะห์และพยากรณ์อย่างไร?

excerpt
การพยากรณ์โดยใช้ข้อมูลเศรษฐกิจที่มีความถี่ต่างกันทำให้การวิเคราะห์เป็นไปอย่างแม่นยำยิ่งขึ้นและเปิดโอกาสให้นักเศรษฐศาสตร์ใช้ข้อมูลที่หลากหลายร่วมกัน แบบจำลองในลักษณะนี้ที่เป็นที่นิยมคือ MIDAS และ VAR บทความนี้นำเสนอผลการเปรียบเทียบความแม่นยำในการพยากรณ์ตัวแปรทางเศรษฐกิจของแบบจำลองทั้งสองเทียบกับแบบจำลองมาตรฐาน
ข้อจำกัดหนึ่งในการวิเคราะห์ข้อมูลเศรษฐกิจมหภาคคือความถี่ของข้อมูลที่แตกต่างกัน ตัวอย่างเช่น การวิเคราะห์ผลกระทบของอัตราเงินเฟ้อรายเดือนต่อผลิตภัณฑ์มวลรวมในประเทศ (GDP) รายไตรมาส ในอดีต การวิเคราะห์ดังกล่าวนี้สามารถทำได้โดยนำข้อมูลอัตราเงินเฟ้อรายเดือนมาหาค่าเฉลี่ยอย่างง่ายเพื่อให้มีความถี่เป็นรายไตรมาสเท่ากันกับข้อมูล GDP วิธีการเฉลี่ยเช่นนี้มีข้อสมมุติสำคัญคือข้อมูลแต่ละเดือนนั้นมีความสำคัญหรือมีน้ำหนักเท่ากันทำให้ค่าเฉลี่ยที่ได้ไม่สะท้อนผลจากข้อมูลรายเดือนที่เกิดขึ้นในไตรมาสก่อน ๆ อย่างไรก็ตาม การเฉลี่ยข้อมูลรายเดือนในไตรมาสอื่น ๆ นั้นอาจทำได้โดยวิธีการเฉลี่ยแบบเคลื่อนที่ (moving average) แต่ค่าเฉลี่ยจากวิธีนี้เป็นค่าที่แสดงถึงแนวโน้มและไม่สะท้อนถึงความผันผวนตามฤดูกาล (seasonality) ซึ่งเป็นคุณลักษณะที่สำคัญของข้อมูลรายเดือน นอกจากนั้น ผลที่ได้จากการวิเคราะห์อาจเกิดจากความสัมพันธ์ลวง (spurious relationship) ซึ่งมิใช่ความสัมพันธ์ที่แท้จริง
ในช่วงประมาณ 20 ปีที่ผ่านมา นักเศรษฐศาสตร์ที่ชื่อ Eric Ghysels จาก University of North Carolina ได้คิดค้นวิธีการนำข้อมูลที่มีความถี่แตกต่างกัน (mixed-frequency) มาวิเคราะห์และพยากรณ์ผ่านแบบจำลองหลายชนิด อาทิ สมการถดถอยที่เรียกว่า MIxed DAta Sampling (MIDAS) และ vector autoregression (VAR) เป็นต้น (โปรดดูรายละเอียดเพิ่มเติมใน Ghysels et al. 2007, Ghysels, 2016 และ Ghysels, 2018) วิธีการเช่นนี้ทำให้การพยากรณ์โดยใช้ข้อมูลที่มีความถี่แตกต่างกันนั้นทำได้ง่ายขึ้นและได้ผลที่แม่นยำยิ่งขึ้น
MIDAS เป็นแบบจำลองที่นิยมใช้กันมากและสามารถหาใช้ได้ในซอฟต์แวร์ทางสถิติและเศรษฐมิติ เช่น R, EViews และ MATLAB เป็นต้น หัวใจสำคัญของ MIDAS คือมีฟังก์ชันที่เฉลี่ย (weight function) ค่าข้อมูลความถี่ที่สูงกว่าหลายรูปแบบ อาทิ normalized beta density with a zero last lag (BT), normalized beta density with a non-zero last lag (BNN), normalized exponential Almon lag polynomial (EAM), unrestricted coefficients (UM), polynomial with step functions (ST) และ Almon lag polynomial of order p (AM) เป็นต้น
ขณะที่ VAR เป็นแบบจำลองที่นำข้อมูลที่มีความถี่แตกต่างกันนั้นมาอยู่ร่วมกันในรูปเวคเตอร์และวิเคราะห์ผ่าน multivariate distribution อย่างไรก็ตาม ข้อจำกัดประการหนึ่งของแบบจำลอง VAR คือสามารถนำมาใช้ได้เฉพาะข้อมูลที่มีความถี่คงที่ เช่น รายไตรมาส รายเดือน แต่ยังไม่สามารถนำมาใช้กับข้อมูลรายวันที่มีจำนวนแตกต่างกันไปในแต่ละเดือนได้
บทความนี้นำเสนอผลการวิเคราะห์และพยากรณ์ข้อมูลเศรษฐกิจมหภาคของไทยที่มีความถี่แตกต่างกันด้วยแบบจำลอง MIDAS และ VAR และเปรียบเทียบผลที่ได้จากแบบจำลองทั้งสองนั้นกับผลจาก autoregressive integrated moving average (ARIMA) ซึ่งเป็นแบบจำลองอนุกรมเวลามาตรฐาน
ข้อมูลความถี่ต่ำที่นำมาวิเคราะห์นั้นประกอบด้วย
- อัตราการเจริญเติบโตทางเศรษฐกิจซึ่งวัดจากอัตราการเปลี่ยนแปลงของ real GDP รายไตรมาส
- อัตราการเปลี่ยนแปลงของจำนวนแรงงานในกำลังแรงงานรายไตรมาส และ
- อัตราเงินเฟ้อรายเดือน
สำหรับข้อมูลความถี่ที่สูงกว่าที่ใช้ในการวิเคราะห์คืออัตราเงินเฟ้อรายเดือน ผลตอบแทนตลาดหุ้นรายวัน (daily stock return) การเปลี่ยนแปลงของอัตราดอกเบี้ยรายวัน และการเปลี่ยนแปลงของอัตราแลกเปลี่ยนรายวัน (รายละเอียดเพิ่มเติมในตารางที่ 1) สำหรับการกำหนดรูปแบบของแบบจำลองนั้น ผู้เขียนได้รวมช่วงเวลาของข้อมูลในระยะเวลาก่อนหน้า (lag) เพื่อวิเคราะห์ความผันผวนตามฤดูกาลทั้งในตัวแปรตั้งต้นหรือตัวแปรตามที่มีความถี่ต่ำกว่าและในตัวแปรที่ใช้พยากรณ์หรือตัวแปรอิสระที่มีความถี่สูงกว่า
ในการพยากรณ์ ผู้เขียนได้จำแนกข้อมูลสำหรับการพยากรณ์ (out-of-sample forecasts) ออกเป็นสองกรณีเพื่อพิจารณาผลจากโรคระบาดโคโรนาไวรัสสายพันธุ์ใหม่ (COVID-19) คือ
- กรณีไม่รวมข้อมูล COVID-19 โดยใช้ข้อมูลสำหรับการพยากรณ์ในปี พ.ศ. 2562 และ
- กรณีรวมข้อมูล COVID-19 โดยใช้ข้อมูลสำหรับการพยากรณ์ในช่วงครึ่งปีหลังของ พ.ศ. 2562 และครึ่งปีแรกของ พ.ศ. 2563 (ซึ่งเป็นช่วงเวลาที่สามารถหาข้อมูลได้ขณะที่ทำการวิเคราะห์)
เหตุที่ใช้ข้อมูลในการพยากรณ์เพียงหนึ่งปีนั้นเนื่องจากผู้เขียนต้องการ
- พยากรณ์ในช่วงเวลาที่สั้นเพื่อแสดงถึงตัวอย่างของการพยากรณ์ปัจจุบัน (nowcasting) และ
- ให้ความผันผวนตามฤดูกาลครบวงรอบ
ในการเปรียบเทียบกับแบบจำลอง ARIMA นั้น ผู้เขียนพิจารณาจากค่าความคลาดเคลื่อนของการพยากรณ์ (forecast errors) เป็นหลัก เกณฑ์ที่ใช้พิจารณาคือค่า mean absolute percentage error (MAPE) และ root mean squared error (RMSE) ซึ่งแบบจำลองที่ให้ค่าที่ต่ำกว่าแสดงถึงแบบจำลองที่ให้ผลการพยากรณ์ที่ดีกว่า ผลการวิเคราะห์และการพยากรณ์ที่ได้มีดังนี้
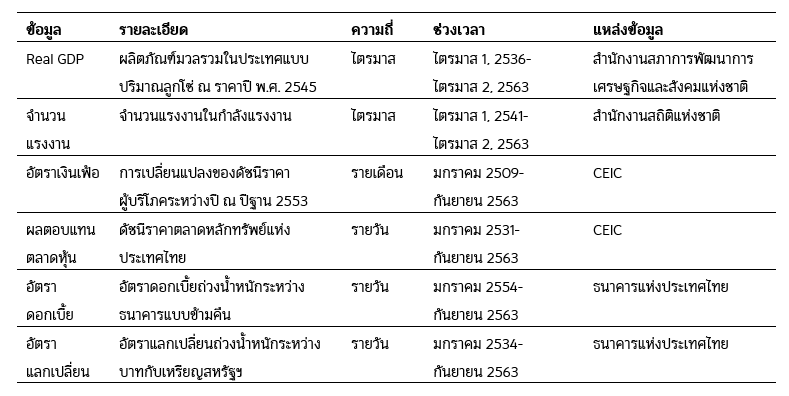
ในกรณีนี้ ตัวแปรอิสระที่ใช้ในการพยากรณ์ประกอบด้วยข้อมูลรายเดือน (อัตราเงินเฟ้อ) และรายวัน (ผลตอบแทนตลาดหุ้น การเปลี่ยนแปลงของอัตราดอกเบี้ย และการเปลี่ยนแปลงของอัตราแลกเปลี่ยน) ในกรณีที่ไม่รวมข้อมูลจาก COVID-19 ในการพยากรณ์พบว่าแบบจำลอง MIDAS ในรูปแบบ ST ที่ใช้ข้อมูลผลตอบแทนตลาดหุ้นรายวันให้ค่าคลาดเคลื่อนจากการพยากรณ์ต่ำสุด สังเกตได้จากเส้น ST(Ret) ภาพที่ 1 ด้านซ้าย ผลดังกล่าวชี้ให้เห็นว่าในสถานการณ์ปกติที่ไม่มี COVID-19 ผลตอบแทนตลาดหุ้นรายวันเป็นตัวแปรที่น่าจะสามารถนำมาใช้พยากรณ์อัตราการเปลี่ยนแปลงของ real GDP รายไตรมาสได้ เหตุที่เป็นเช่นนี้น่าจะมาจากการรับรู้ข้อมูลข่าวสารและปฏิกิริยาของผู้บริโภคซึ่งสะท้อนออกไปในตลาดหุ้นได้ค่อนข้างเร็ว
ขณะที่ผลการพยากรณ์ในกรณีที่รวมข้อมูล COVID-19 พบว่าแบบจำลอง MIDAS ในรูปแบบ UM ที่ใช้ข้อมูลอัตราเงินเฟ้อรายเดือนหรือ UM(Inf) ในภาพที่ 2 ด้านขวาและแบบจำลอง VAR ที่ใช้ข้อมูลอัตราเงินเฟ้อเป็นแบบจำลองที่ให้ค่าความคลาดเคลื่อนจากการพยากรณ์ต่ำสุดโดยที่ MIDAS ให้ค่า MAPE ต่ำที่สุด (มิได้นำเสนอในบทความนี้) ขณะที่ VAR ให้ค่า RMSE ต่ำที่สุด ผลที่ได้สะท้อนให้เห็นถึงผลกระทบจาก COVID-19 ที่ทำให้อุปสงค์โดยรวมลดลงอย่างมากจนทำให้ระดับราคา (เงินเฟ้อ) และอัตราการเจริญเติบโตทางเศรษฐกิจลดลงไปอย่างมากเช่นเดียวกัน ด้วยเหตุนี้ทำให้อัตราเงินเฟ้อเป็นตัวพยากรณ์ที่ดีที่สุด กรณีของผลตอบแทนตลาดหุ้นที่ไม่ได้ให้ค่าพยากรณ์ที่ดีที่สุดอาจเป็นไปได้ว่าหลังจากที่ดัชนีราคาลดลงอย่างมากในช่วงเดือนมกราคม-กุมภาพันธ์ พ.ศ. 2563 หลังจากนั้นได้เริ่มปรับตัวขึ้นอย่างช้า ๆ อย่างต่อเนื่อง ขณะที่อัตราเงินเฟ้อและอัตราการเจริญเติบโตทางเศรษฐกิจยังคงลดลงในไตรมาสที่ 2
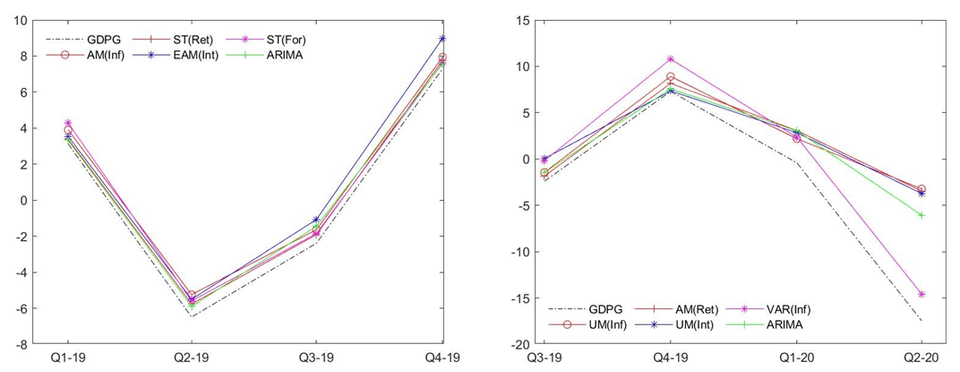
แบบจำลองและตัวแปรอิสระที่ใช้ในการพยากรณ์ยังคงเป็นเช่นดียวกับกรณีของ real GDP ข้างต้น ผลการพยากรณ์ที่ได้ในกรณีไม่รวมข้อมูล COVID-19 พบว่าแบบจำลอง MIDAS ในรูปแบบ EAM ที่ใช้การเปลี่ยนแปลงของอัตราดอกเบี้ยรายวันให้ค่า MAPE ต่ำที่สุด ขณะที่แบบจำลอง VAR นั้นให้ค่า RMSE ต่ำที่สุด สิ่งที่น่าสนใจจากการพิจารณาภาพที่ 2 ด้านซ้ายมือคือแบบจำลอง VAR นั้นสามารถพยากรณ์ความผันผวนตามฤดูกาลได้ดีกว่าแบบจำลองอื่น ๆ ความผันผวนตามฤดูกาลที่เกิดขึ้นอย่างชัดเจนนี้เป็นลักษณะเฉพาะของตลาดแรงงานไทยซึ่งสอดคล้องกับผลการศึกษาของยงยุทธและคณะ (2563) ด้วยเหตุนี้แบบจำลอง VAR น่าจะเป็นแบบจำลองที่เหมาะสมในกรณีที่ไม่รวมข้อมูล COVID-19 นี้
สำหรับกรณีของผลการพยากรณ์ที่รวมข้อมูล COVID-19 นั้น แบบจำลอง MIDAS ในรูปแบบ AM ที่ใช้ข้อมูลอัตราการเปลี่ยนแปลงอัตราแลกเปลี่ยนรายวันให้ค่า MAPE ต่ำที่สุด ขณะที่แบบจำลอง MIDAS ในรูปแบบ ST ที่ใช้ข้อมูลการเปลี่ยนแปลงอัตราดอกเบี้ยรายวันให้ค่า RMSE ต่ำที่สุด แม้ว่าผลที่ได้อาจจะไม่สามารถนำมาอธิบายเหตุผลทางเศรษฐศาสตร์ได้อย่างชัดเจนนัก แต่ข้อสรุปประการหนึ่งที่ได้คือการใช้ข้อมูลรายวันมาพยากรณ์ผ่านแบบจำลอง MIDAS ช่วยให้ได้ค่าพยากรณ์ที่ดีที่สุด อย่างไรก็ตาม ประเด็นการวิจัยเชิงเทคนิคที่น่าดำเนินการคือการพัฒนาแบบจำลอง VAR เพื่อนำข้อมูลรายวันมาร่วมวิเคราะห์
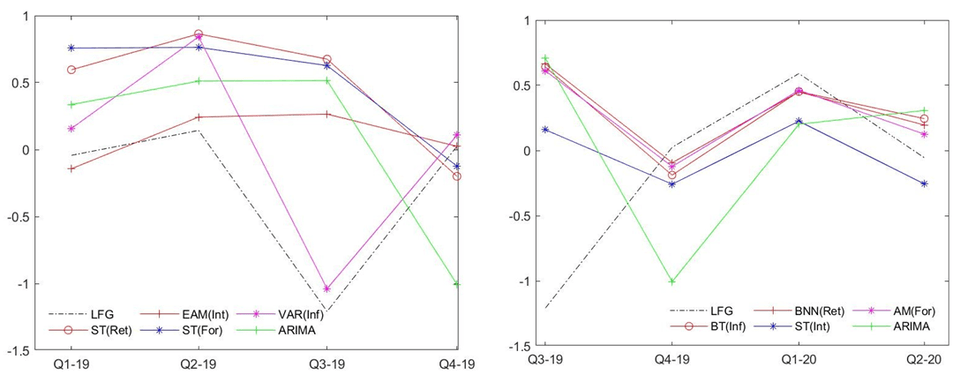
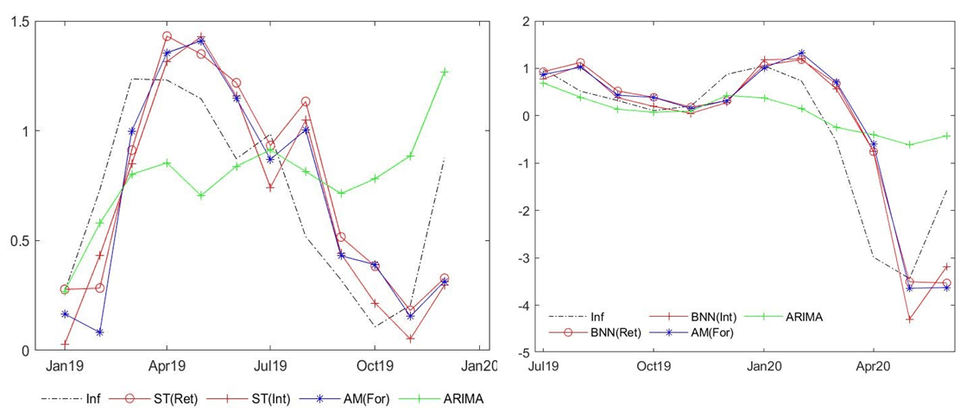
ในกรณีนี้แบบจำลองที่สามารถนำมาวิเคราะห์ได้มีเพียง MIDAS (และ ARIMA ซึ่งเป็นแบบจำลองมาตรฐาน) เนื่องจากแบบจำลอง VAR นั้นยังไม่สามารถวิเคราะห์ข้อมูลรายวันที่มีจำนวนวันแตกต่างกันไปในแต่ละเดือนได้ ขณะที่ตัวแปรอิสระที่ใช้ในการพยากรณ์นั้นเป็นข้อมูลรายวัน (ซึ่งมีความถี่สูงกว่า) ผลการพยากรณ์ในกรณีไม่รวมข้อมูล COVID-19 พบว่าแบบจำลอง MIDAS ในรูปแบบ ST ที่ใช้ข้อมูลการเปลี่ยนแปลงอัตราดอกเบี้ยให้ค่า MAPE และ RMSE ต่ำที่สุด (ประเมินจากภาพที่ 3 ด้านซ้าย) ผลที่ได้แสดงให้เห็นว่าในกรณีสถานการณ์ปกติที่ไม่มี COVID-19 อัตราดอกเบี้ยรายวันเป็นเครื่องมือทางนโยบายที่สามารถนำมาใช้ควบคุมอัตราเงินเฟ้อได้เนื่องจากเป็นปัจจัยที่ให้ค่าพยากรณ์ต่ำที่สุด
ขณะที่ผลการพยากรณ์ในกรณีที่รวมข้อมูล COVID-19 พบว่าแบบจำลอง ARIMA ซึ่งเป็นแบบจำลองมาตรฐานให้ค่าพยากรณ์ที่ดีที่สุด (ค่าคลาดเคลื่อนจากการพยากรณ์ต่ำที่สุด) อย่างไรก็ตาม สิ่งที่ควรระมัดระวังในกรณีนี้คือหากพิจารณาภาพที่ 3 ด้านขวาพบว่าแบบจำลอง ARIMA ไม่สามารถพยากรณ์ความผันผวนตามฤดูกาลได้ดีนักโดยเฉพาะตั้งแต่เกิด COVID-19 ในเดือนมกราคม พ.ศ. 2563 นั่นหมายความว่าหากการพยากรณ์ครอบคลุมระยะเวลาของข้อมูลที่ยาวนานขึ้นโดยเฉพาะเมื่อโรคระบาด COVID-19 จบสิ้นลง ผลการพยากรณ์และข้อสรุปที่ได้น่าจะชัดเจนขึ้น
ผลจากการวิเคราะห์และพยากรณ์ข้างต้นแสดงให้เห็นว่าการพยากรณ์ข้อมูลเศรษฐกิจมหภาคของไทยผ่านแบบจำลองที่ใช้ข้อมูลที่มีความถี่แตกต่างกันน่าจะช่วยให้ได้ค่าพยากรณ์ที่ดีขึ้น นอกจากนั้นแล้ว ผลการวิเคราะห์ยังอาจช่วยทำให้เห็นความสัมพันธ์ระหว่างตัวแปรหรือปัจจัยที่มีความถี่แตกต่างกันชัดเจนยิ่งขึ้น ข้อสรุปและนัยยะทางเศรษฐกิจที่ได้อาจช่วยให้การออกนโยบายและมาตรการในการจัดการเศรษฐกิจมหภาคเป็นไปอย่างมีประสิทธิภาพ
note
บทความนี้เป็นบทความเชิงสังเคราะห์จากโครงการวิจัยเรื่อง “การวิเคราะห์และพยากรณ์ข้อมูลเศรษฐกิจมหภาคของไทยที่มีความถี่แตกต่างกัน” สนับสนุนทุนวิจัยโดยสถาบันเศรษฐกิจป๋วย อึ๊งภากรณ์
ยงยุทธ แฉล้มวงษ์, อัมมาร สยามวาลา, ณัฐนันท์ วิจิตรอักษร, อลงกรณ์ ฉลาดสุข, โชคชัยชาญ วิโรจน์สัตตบุษย์, ขวัญกมล ถนัดค้า และเกศินี ธารีสังข์. 2563. การจัดทําดัชนีชี้วัดภาวะตลาดแรงงานของประเทศไทย. รายงานวิจัยฉบับสมบูรณ์เสนอต่อสํานักงานคณะกรรมการส่งเสริมวิทยาศาสตร์ วิจัยและนวัตกรรม. กรุงเทพฯ: สถาบันวิจัยเพื่อการพัฒนาประเทศไทย.Ghysels, E. 2016. Macroeconomics and the reality of mixed-frequency data. Journal of Econometrics. 193, 294–314.
Ghysels, E. 2018. Mixed-frequency models. Oxford Research Encyclopedias: Economics and Finance. DOI: 10.1093/acrefore/9780190625979.013.176
Ghysels, E., Sinko, A., and Valkanov, R. 2007. MIDAS regressions: Further results and new directions. Econometric Reviews. 26(1), 53–90.