ความเสี่ยงต่อระบบและการลุกลามของวิกฤตการณ์การเงิน

การลุกลามของวิกฤตการณ์การเงิน (financial contagion) เป็นสิ่งที่ผู้ดำเนินนโยบายให้ความสำคัญและพยายามสร้างตัวชี้วัดที่เหมาะสมขึ้น เพื่อใช้เป็นเครื่องมือในการเฝ้าระวังและตรวจสอบความเสี่ยงที่มีต่อระบบการเงินและเศรษฐกิจ ความเสี่ยงต่อระบบ (systemic risk) หมายถึงความเสี่ยงที่ระบบการเงินจะเกิดความเสียหายในวงกว้างทั้งระบบ และส่งผลให้เกิดการชะลอตัวของเศรษฐกิจอย่างรุนแรง ซึ่งแตกต่างจากความเสี่ยงที่เป็นระบบ (systematic risk) ที่หมายถึงความเสี่ยงที่จะเกิดขึ้นกับเฉพาะบุคคลหรือเฉพาะองค์กรเท่านั้น โดยไม่ได้เกิดการลุกลามต่อไปยังส่วนอื่น ตัวอย่างเหตุการณ์ของความเสี่ยงต่อระบบที่เห็นได้ชัด เช่น วิกฤตการณ์การเงิน Black Monday ในปี 1987 โดยมีจุดเริ่มต้นจากการเทขายอย่างหนักในตลาดหุ้นประเทศสหรัฐอเมริกา แล้วเกิดการลุกลามอย่างรวดเร็วไปสู่ตลาดหุ้นประเทศอื่น ๆ สร้างความเสียหายอย่างรุนแรงแก่เศรษฐกิจโลก สำหรับผู้ดำเนินนโยบาย คำถามสำคัญก็คือเราจะสามารถวัดความเสี่ยงและจำกัดความเสียหายในวงกว้างนี้ได้อย่างไรเมื่อวิกฤตการณ์การเงินเกิดขึ้น เพื่อรักษาเสถียรภาพของระบบเศรษฐกิจของประเทศ

ตลาดการเงินมีความเปราะบางต่อทั้งจากปัจจัยภายในและภายนอกที่เข้ามากระทบ แบบจำลองส่วนใหญ่มักจะกำหนดให้ตัวแปร shock ต่าง ๆ เป็น shock ที่เกิดมาจากภายนอก (exogenous shock) ซึ่งแตกต่างจากแนวคิดพื้นฐานของการศึกษาในบทความนี้ ที่มองว่าความเสี่ยงต่อระบบเกิดขึ้นจากภายในตัวของระบบเอง กล่าวคือ เมื่อส่วนใดส่วนหนึ่งของระบบการเงินมี shock เกิดขึ้น (endogenous shock) ความเสียหายตรงจุดนั้นจะก่อให้เกิดการลุกลามไปยังส่วนอื่นทั่วทั้งระบบ ความเสี่ยงต่อระบบแบบที่กล่าวถึงนี้ สามารถศึกษาได้โดยการประยุกต์ใช้วิธีการทางสถิติที่เรียกว่า extreme value theory (EVT) ในช่วงเริ่มแรก EVT ถูกนำมาใช้ศึกษาเกี่ยวกับเหตุการณ์ภัยพิบัติทางธรรมชาติ ต่าง ๆ เช่น ในประเทศเนเธอแลนด์ พื้นที่มากกว่า 40% อยู่ต่ำกว่าระดับน้ำทะเล ในอดีตต้องเผชิญกับปัญหาน้ำท่วมและอุทกภัยอย่างหนัก ผู้เชี่ยวชาญจึงได้นำ EVT มาใช้เพื่อช่วยตอบคำถามสำคัญ อาทิ ความสูงของเขื่อนกั้นพายุที่เหมาะสมควรเป็นเท่าไร เพื่อให้โอกาสในการเกิดน้ำท่วมเท่ากับ 1 ใน 10,000 ปี ในช่วงทศวรรษที่ผ่านมา EVT ได้ถูกนำมาประยุกต์ใช้ทางการเงินและเศรษฐศาสตร์แพร่หลายมากขึ้น

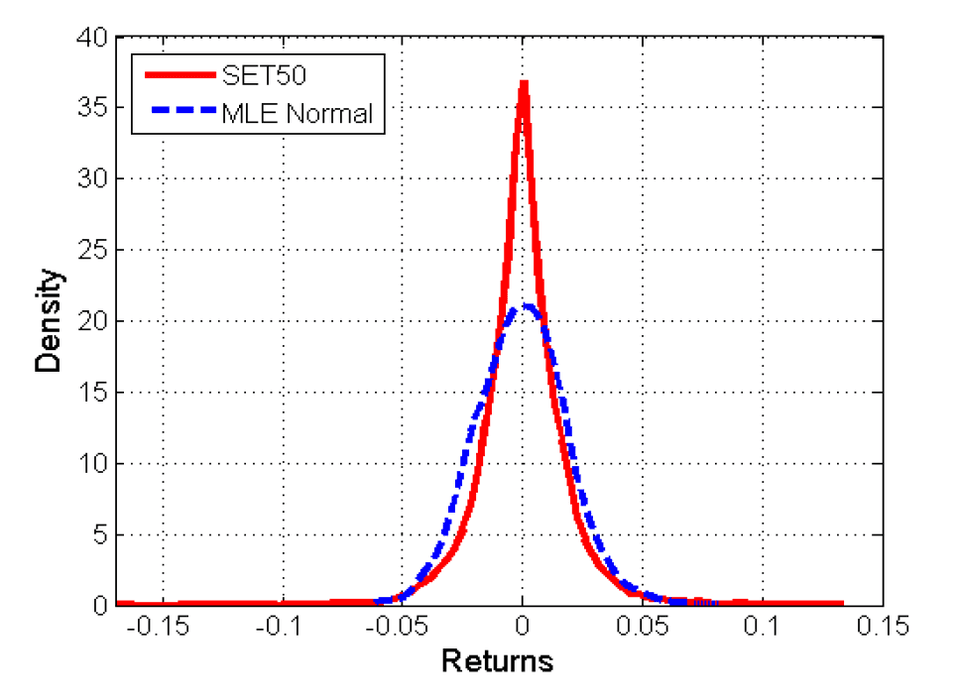
สาเหตุสำคัญที่เรานำวิธีการ EVT มาใช้ในการศึกษาวิกฤตการณ์การเงินนั้น คงต้องมาเริ่มกันที่แนวคิดพื้นฐานในเรื่องของ “fat-tail” distribution ในการศึกษาเหตุการณ์ที่มีโอกาสเกิดขึ้นได้ยาก (rare event) อย่างเช่นวิกฤตการณ์การเงิน คือเรากำลังสนใจศึกษาเหตุการณ์ที่มีโอกาสในการเกิดต่ำมาก เช่น worst case event ต่าง ๆ จากข้อเท็จจริงที่พบได้จากการวิเคราะห์ข้อมูลเบื้องต้นของการศึกษาอื่นทั่วไป พบว่า ผลตอบแทนของสินทรัพย์และข้อมูลทางเศรษฐกิจมหภาคต่าง ๆ ส่วนใหญ่ไม่ได้มีการกระจายตัวแบบปกติ (normal distribution) ซึ่งเป็นสมมติฐานพื้นฐานสำคัญของหลายแบบจำลองที่ใช้กันอยู่ในปัจจุบัน ยกตัวอย่างเช่น หากพิจารณาผลตอบแทนรายวันของตลาดหุ้นไทย (SET 50 index) ตั้งแต่ปี 1995 ถึง 2013 แล้วสร้างแบบการกระจายตัวขึ้น ดังแสดงในรูปที่ 1 เราจะเห็นได้อย่างชัดเจนว่า tail ทั้งสองด้าน คือด้าน loss และด้าน gain มีลักษณะยาวมาก ซึ่งถ้าใช้ normal distribution มา fit ข้อมูลชุดนี้ (แสดงด้วยเส้นประ) เราจะไม่สามารถสร้างผลของแบบจำลองที่มีลักษณะ tail แบบเดียวกับของข้อมูลที่เกิดขึ้นจริงได้ การใช้เครื่องมือที่อยู่บนสมมุติฐานของ normal distribution มาใช้จึงทำให้การประเมินความเสี่ยงที่เกิดขึ้นต่ำกว่าที่เป็นจริง นอกจากนี้ ข้อดีของ EVT อีกประการก็คือ เป็นวิธีที่นำเฉพาะข้อมูล extreme มาใช้ในการศึกษา ซึ่งหมายความว่า ข้อมูลที่ใกล้ค่าเฉลี่ยจะไม่ถูกนำมาใช้ ซึ่งเหมาะแก่การศึกษาในเรื่องของวิกฤตการณ์ต่าง ๆ และการลุกลามได้เป็นอย่างดี

ในการหาความสัมพันธ์ระหว่างวิกฤตการณ์การเงินที่เกิดขึ้นในสองประเทศ โดยมากผู้ศึกษามักจะเลือกเครื่องมือที่อิงกับการใช้ correlation เพื่อวิเคราะห์ความสัมพันธ์ อย่างไรก็ดี ในการศึกษาเหตุการณ์ที่เกิดขึ้นยาก การใช้ correlation ยังมีข้อจำกัดอยู่หลายประการ (Embrechts et al., 1999) เช่น ในทางทฤษฎี correlation มีความเกี่ยวข้องกับสมมุติฐานเรื่อง normal distribution ซึ่งทำให้ผลลัพธ์ที่ได้มีค่าต่ำกว่าความเป็นจริง นอกจากนี้ การนำ correlation มาใช้วิเคราะห์ความสัมพันธ์ตรงจุดการกระจายตัวบริเวณ tail มักจะให้ผลการศึกษาที่ไม่แน่นอน (Ang and Chen 2000) และค่า correlation ที่คำนวณได้ ยังไม่สามารถสื่อถึงโอกาสความเป็นไปได้ของการเกิดวิกฤตการณ์และการลุกลาม

โดยใช้แนวคิดในเรื่องของ EVT เรานำเสนอเครื่องมือประเภท non-parametric ที่สามารถคำนวณหาค่าความเป็นไปได้ของการเกิดการลุกลามของวิกฤตการณ์การเงินได้โดยตรง โดยไม่ต้องมีสมมติฐานใด ๆ เกี่ยวกับการกระจายตัวของข้อมูล ซึ่งก็คือ ดรรชนีชี้วัดความเสี่ยงต่อระบบ (systemic risk indicator) (De Vries, 2005) สมมุติให้ $X$ และ $Y$ คือผลตอบแทนของตลาดหุ้นของสองประเทศ โดยมีระดับผลตอบแทน ณ จุดการเกิดวิกฤต อยู่ที่ $s$¹ ดังนั้น ความเป็นไปได้ที่ตลาดหุ้นของทั้งสองประเทศจะเกิดวิกฤตการณ์การเงินขึ้นพร้อมกัน หากตลาดหุ้นของประเทศใดประเทศหนึ่งเกิดวิกฤตขึ้น สามารถเขียนสมการได้เป็น

ทั้งนี้ ดรรชนีชี้วัดความเสี่ยงต่อระบบนี้ สามารถใช้เพื่อศึกษาการลุกลามของวิกฤตการณ์การเงินมากกว่าสองประเทศพร้อมกันได้ (Hartmann et al., 2004)

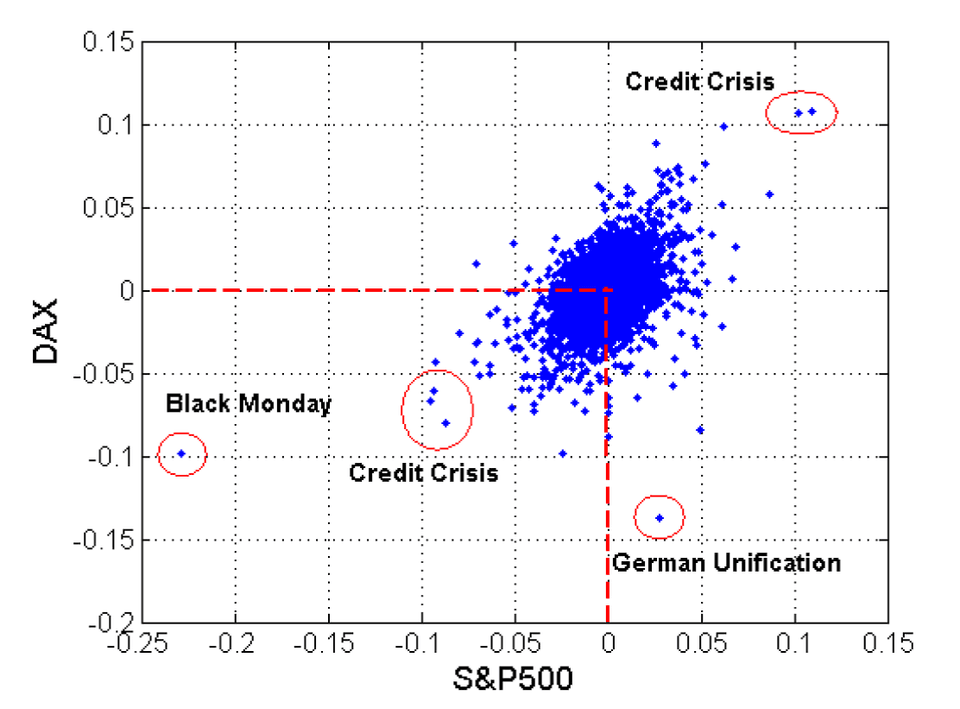
เพื่อให้เข้าใจถึงการนำดรรชนีชี้วัดความเสี่ยงต่อระบบมาใช้ เราพิจารณาข้อมูลตลาดทุนของประเทศสหรัฐอเมริกา (S&P 500) และเยอรมัน (DAX)

รูปที่ 2 แสดงแผนภาพการกระจายของผลตอบแทนรายวันของตลาดทุนของทั้งสองประเทศ จากรูปจะเห็นได้ว่า ในช่วงตั้งแต่ปี 1973 ถึง 2013 มีวิกฤตการณ์การเงินเกิดขึ้นอยู่หลายครั้ง ไม่ว่าจะเป็นในกรณีที่ทั้งสองตลาดเคลื่อนไหวไปในทิศทางเดียวกัน เช่น Black Monday ในปี 1987 และ Credit Crisis ในปี 2008 หรือในกรณีที่เกิดวิกฤตเฉพาะในประเทศเดียว เช่น ช่วงที่เยอรมันมีการรวมประเทศเกิดขึ้น ในปี 1990 จากข้อมูลชุดนี้ สิ่งที่เรากำลังสนใจศึกษาก็คือ ความสัมพันธ์ของ extreme large loss หรือข้อมูลในส่วนของควอดรันต์ด้านล่างซ้าย

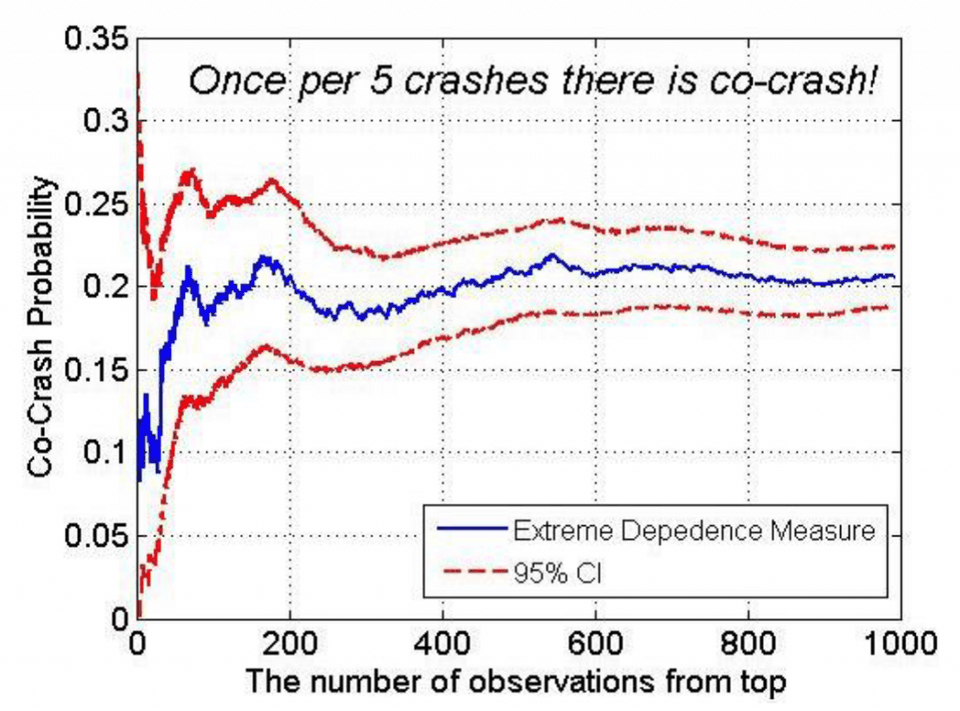
สำหรับการคำนวณดรรชนีชี้วัดความเสี่ยงต่อระบบ เริ่มต้นด้วยการเรียงลำดับข้อมูลแต่ละชุดจากมากไปหาน้อย แล้วกำหนดระดับค่าวิกฤต s ของแต่ละตัวแปร โดยใช้ค่าจากข้อมูลของตัวมันเอง (empirical threshold) จากนั้น ไล่ลำดับ $s$ จากค่าสูงสุดลงมา โดยที่ระดับ $s$ หนึ่ง ๆ เราจะสามารถคำนวณหาดรรชนีชี้วัดความเสี่ยงต่อระบบได้

รูปที่ 3 แสดงค่าของดรรชนีชี้วัดความเสี่ยงต่อระบบที่คำนวณได้ ณ จุดวิกฤต s ต่าง ๆ ทั้งนี้ จุดวิกฤตที่เหมาะสมคือจุดที่ค่าดรรชนีเริ่มตั้งระดับอยู่ที่ค่าค่าหนึ่ง² จากรูปเราจะได้ว่า ความเป็นไปได้ของการเกิดการลุกลามของวิกฤตการณ์การเงินของตลาดทุนระหว่างสหรัฐอเมริกาและเยอรมันนั้นอยู่ที่ประมาณ 0.2 ซึ่งสามารถอธิบายได้อีกนัยหนึ่งว่า ใน 5 ครั้งของการเกิดวิฤตการณ์เงินในสหรัฐอเมริกาหรือเยอรมัน หนึ่งครั้งจะเป็นวิกฤตการณ์ที่เกิดการลุกลาม³

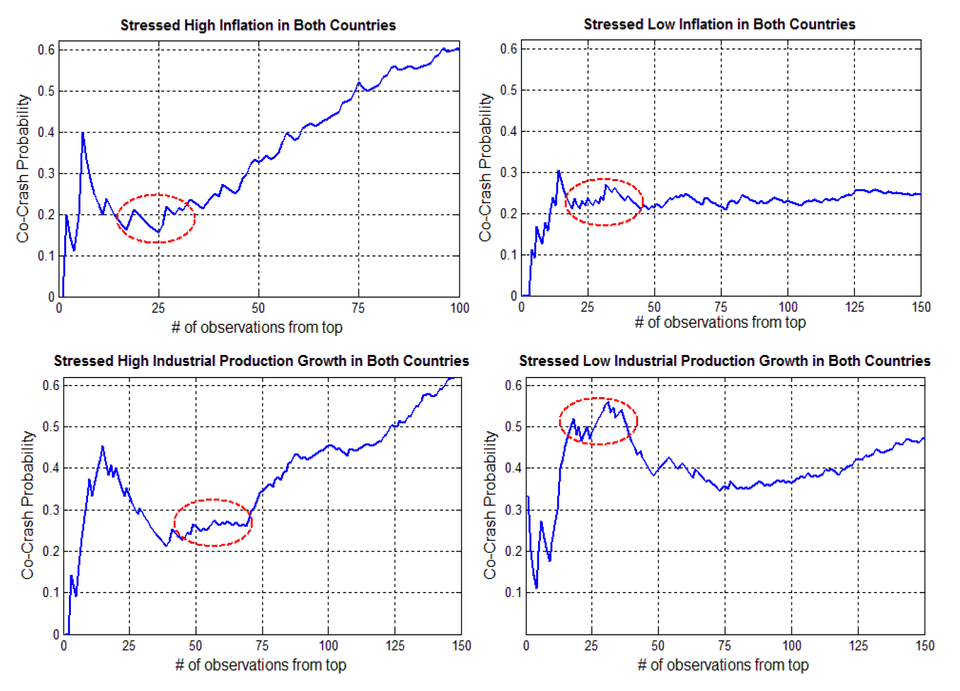
เพื่อให้การศึกษาสามารถเชื่อมต่อไปถึงนัยยะเชิงนโยบาย เราได้ทำการศึกษาการลุกลามวิกฤตการณ์การเงิน ในช่วงเวลาเฉพาะที่ อัตราเงินเฟ้อ (inflation) และอัตราการเติบโตของผลผลิตอุตสาหกรรม (industrial production growth) ของสหรัฐอเมริกาและเยอรมันอยู่ในระดับวิกฤต โดยสองตัวแปรนี้ เป็นปัจจัยพื้นฐานทางเศรษฐกิจมหภาคที่สำคัญในด้านอุปสงค์และอุปทาน ตามลำดับ⁴ สำหรับการศึกษา เราจะพิจารณาการลุกลามวิกฤตการณ์การเงิน ในเงื่อนไขที่ตัวแปรเศรษฐกิจมหภาคของทั้งสองประเทศอยู่ในระดับวิกฤตทั้งในด้านต่ำและด้านสูง โดยระดับวิกฤตที่ใช้ คือค่าที่ 5% และ 95% quantile ของค่าเคลื่อนที่ 10 ปี ของข้อมูลรายเดือน

รูปที่ 4 แสดงค่าดรรชนีชี้วัดความเสี่ยงต่อระบบที่คำนวณจากข้อมูลผลตอบแทนรายวันของตลาดทุนในสหรัฐอเมริกาและเยอรมัน ในช่วงที่อัตราเงินเฟ้อและอัตราการเติบโตของผลผลิตอุตสาหกรรมอยู่ในระดับวิกฤต จากรูปจะเห็นได้ว่า ความเป็นไปได้ของการลุกลามวิกฤตการณ์การเงินในสภาวะวิกฤตของอัตราเงินเฟ้อทั้งในระดับต่ำและระดับสูง ไม่ได้แตกต่างไปจากผลที่ได้ในช่วงปกติ (รูปที่ 3) มากนัก หรืออาจกล่าวได้ว่า อัตราเงินเฟ้อหรือปัจจัยที่เกี่ยวข้องกับนโยบายการเงินไม่ได้ส่งผลถึงการลุกลามวิกฤตการณ์การเงินของสองประเทศ อย่างไรก็ดี เมื่อพิจารณาในส่วนของอัตราการเติบโตผลผลิตอุตสาหกรรม โดยเฉพาะในกรณีที่เกิดการหดตัวอย่างรุนแรงพร้อมกันของทั้งสองประเทศ กลับพบว่า โอกาสการเกิดการลุกลามวิกฤตการณ์การเงินเพิ่มสูงขึ้นไปถึง ประมาณ 0.5 ซึ่งหมายถึงปัจจัยทางเศรษฐกิจด้านอุปทานเป็นตัวขับเคลื่อนสำคัญที่ทำให้เกิดการลุกลาม

บทความนี้นำเสนอวิธีการวัดความเป็นไปได้ของการเกิดการลุกลามวิกฤตการณ์การเงิน โดยใช้ดรรชนีชี้วัดความเสี่ยงต่อระบบ ซึ่งเป็นการนำทฤษฎี extreme value theory มาประยุกต์ใช้ โดยได้ทำการศึกษาการลุกลามวิกฤตการณ์การเงินทั้งในสภาวะทั่วไปและสภาวะที่ปัจจัยพื้นฐานทางเศรษฐกิจมหภาคอยู่ในระดับวิกฤต ในการศึกษานี้ อัตราเงินเฟ้อมีบทบาทสำคัญในฝั่งเศรษฐกิจด้านอุปสงค์ และอัตราการเติบโตของผลผลิตอุตสาหกรรมเป็นตัวแปรสำคัญด้านอุปทาน จากการศึกษาในกรณีของตลาดทุนของประเทศพัฒนาแล้วอย่างสหรัฐอเมริกาและเยอรมัน พบว่า ปัจจัยที่เกี่ยวข้องกับนโยบายการเงินอย่างอัตราเงินเฟ้อไม่ได้ส่งผลต่อการลุกลามของวิกฤตการณ์การเงินเท่าไรนัก ซึ่งสาเหตุหนึ่งอาจเนื่องมาจากการที่มีอัตราแลกเปลี่ยนช่วยในการแบกรับผลกระทบของ shock ต่าง ๆ ที่เกิดขึ้น ที่น่าสนใจก็คือ ปัจจัยที่เกี่ยวข้องกับเศรษฐกิจจริง เช่น อัตราการเติบโตของผลผลิตอุตสาหกรรม เป็นส่วนสำคัญที่ผลักดันให้เกิดการลุกลามวิกฤตการณ์การเงิน ซึ่งผู้ดำเนินนโยบายควรต้องคอยเฝ้าระวังและจับตามองอย่างใกล้ชิดเพื่อรักษาเสถียรภาพของระบบการเงิน

Ang A. and Chen J. (2002). Asymmetric Correlations of Equity Portfolios. Journal of Financial Economics 63: 443–494

Embrechts P., McNeil A. and Straumann D. (1999). Correlation: Pitfalls and Alternatives. Risk 12: 69–71.

De Vries C.G. (2005). The Simple Economics of Bank Fragility. Journal of Banking and Finance 29: 803–825.

Hartmann P., Straetmans S. and de Vries C.G. (2004). Asset Market Linkages in Crisis Periods. Review of Economics and Statistics 86: 313–326.

Leuwattanachotinan C. and de Vries C.G. (2015). Extreme Linkages in Financial Markets: Macro Shocks and Systemic Risk. PIER Discussion Paper 2/2015.