วิกฤตค่าเงินบาท.. เรื่องเล่าจากส่วนหางของการกระจาย

excerpt
การสร้างเสถียรภาพทางเศรษฐกิจ คือ การหลีกเลี่ยงการเกิดวิกฤตการเงินและวิกฤตเศรษฐกิจอื่น ๆ ซึ่งหมายรวมถึงการป้องกันการเกิดอัตราเงินเฟ้อในระดับสูงและความผันผวนของตลาดการเงินและค่าเงินที่มากเกินพอดี (IMF, 2008) วิกฤตค่าเงิน (Currency Crisis) เป็นปัจจัยหนึ่งที่สามารถบั่นทอนการเจริญเติบโตและเสถียรภาพทางเศรษฐกิจของประเทศ แม้ว่าในปัจจุบันโอกาสการเกิดวิกฤตค่าเงินจะอยู่ในระดับต่ำและอาจไม่ใช่ข้อกังวลของภาครัฐ แต่การนำ Extreme Value Theory (EVT) เข้ามาใช้ในการศึกษา Tail Risk ของเงินบาทช่วยเปลี่ยน “unknown unknowns” ให้เป็น “known unknowns” เพื่อรักษาเสถียรภาพทางเศรษฐกิจ
บทความนี้ศึกษาโอกาสการเกิดวิกฤตค่าเงินและหาปัจจัยทางเศรษฐศาสตร์ที่สามารถช่วยพยากรณ์การเกิดวิกฤตค่าเงินโดยนำ EVT เข้ามาใช้ในการกำหนดการเกิดวิกฤตค่าเงินบาท และบ่งชี้การเปลี่ยนแปลงที่ผิดปกติของปัจจัยทางเศรษฐศาสตร์ เพื่อศึกษาว่าการเคลื่อนไหวที่ผิดปกติของปัจจัยทางเศรษฐศาสตร์ใดสามารถใช้เป็นตัวพยากรณ์การเกิดวิกฤตค่าเงินบาท ซึ่งผลการศึกษาแสดงให้เห็นว่า ปัจจัยทางเศรษฐศาสตร์ที่มักใช้ในการพยากรณ์วิกฤตค่าเงินขาดความน่าเชื่อถือเมื่อนำไปใช้พยากรณ์การเกิดวิกฤตค่าเงินขนาดใหญ่ และวิธีของ EVT สามารถเลือกตัวพยากรณ์วิกฤตค่าเงินได้ดีกว่าแบบจำลอง Probit ที่ใช้กันอยู่โดยทั่วไป1
แต่ละคนอาจมีคำตอบที่แตกต่างกันไป คนส่วนใหญ่ทราบเมื่อได้ยินข่าวการเปลี่ยนแปลงของอัตราแลกเปลี่ยนที่รวดเร็วและรุนแรง ส่วนในทางวิชาการนั้น การบ่งชี้ว่าเงินสกุลหนึ่ง ๆ กำลังเผชิญวิกฤตหรือไม่ มีข้อที่ต้องนำมาพิจารณา 2 ประการ ประการแรก คือ ปัจจัยที่สะท้อนปัญหาหรือโอกาสการเกิดวิกฤตค่าเงิน และประการที่สอง คือ ระดับการเปลี่ยนแปลงของปัจจัยเหล่านั้น ระดับใดจึงถือว่าวิกฤต
บทความนี้พิจารณาวิกฤตค่าเงินโดยใช้ดัชนี Exchange Market Pressure (EMP) จากงานของ Eichengreen, Rose and Wyplosz (1996) ซึ่งเป็นค่าเฉลี่ยถ่วงน้ำหนักที่สร้างขึ้นจากตัวแปร 3 ตัว ได้แก่ อัตราการเปลี่ยนแปลงอัตราแลกเปลี่ยน ระดับการเปลี่ยนแปลงอัตราดอกเบี้ยภายในประเทศเทียบกับต่างประเทศ ลบด้วยอัตราการเปลี่ยนแปลงทุนสำรองระหว่างประเทศเทียบกับต่างประเทศ
แนวคิดของดัชนี EMP คือ แม้ว่าการเปลี่ยนแปลงของอัตราแลกเปลี่ยนจะสะท้อนปัญหาค่าเงินได้อย่างค่อนข้างชัดเจน แต่อาจไม่ใช่ทั้งหมด เพราะในหลายกรณีมีการดำเนินการของทางการเพื่อรักษาไม่ให้ค่าเงินเปลี่ยนแปลง เช่น เพื่อป้องกันการอ่อนค่าของเงิน ทางการอาจขายทุนสำรองระหว่างประเทศและ/หรือเพิ่มอัตราดอกเบี้ยเพื่อเพิ่มอุปสงค์ต่อเงินภายในประเทศ การดำเนินการเหล่านี้อาจแสดงถึงปัญหาที่นำไปสู่วิกฤตค่าเงินได้เช่นกัน ดังนั้นดัชนี EMP จึงได้นำการเปลี่ยนแปลงปริมาณทุนสำรองระหว่างประเทศและอัตราดอกเบี้ยเข้ามาร่วมในการบ่งชี้การเกิดวิกฤตค่าเงิน
ส่วนการเคลื่อนไหวของดัชนี EMP ในระดับใดจึงจะถือว่าเป็นวิกฤตนั้น ขึ้นอยู่กับมุมมองของแต่ละบุคคล โดยงานที่ศึกษาวิกฤตค่าเงินส่วนใหญ่มักกำหนดให้การเคลื่อนไหวของดัชนี EMP ที่ห่างจากค่าเฉลี่ย (Mean) เกินไปกว่า 1.5, 2 หรือ 3 ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) เป็นวิกฤตค่าเงิน
บทความนี้ได้นำ EVT เข้ามาใช้ในการกำหนดวิกฤตค่าเงิน โดยแบ่งการกระจาย (Distribution) ออกเป็นส่วนกลางและส่วนหาง แล้วกำหนดให้การเคลื่อนไหวของดัชนี EMP ที่อยู่ในช่วงกลางของการกระจาย ซึ่งเป็นการเคลื่อนไหวที่มีขนาดไม่ใหญ่มากและเกิดขึ้นบ่อยครั้งเป็นการเคลื่อนไหวแบบปกติ ส่วนการเคลื่อนไหวในส่วนหางของการกระจายเป็นวิกฤตค่าเงิน เพราะเป็นระดับของดัชนีที่แม้จะเกิดขึ้นนานครั้งแต่มีขนาดใหญ่เกินปกติ (Rare Event) จึงอาจก่อให้เกิดผลเสียต่อระบบเศรษฐกิจโดยรวม
Extreme Value Theory (EVT) เป็นทฤษฎีที่ศึกษาส่วนหางของการกระจาย โดยมีใจความสำคัญว่า ไม่ว่าข้อมูลจะมี Data Generating Process ในรูปแบบใด ข้อมูลในส่วนหางของการกระจายจะมี Asymptotic Distribution ที่เป็นไปได้ 3 รูปแบบ คือ หางบาง (เช่น การกระจายแบบปกติ หรือ Normal) หางอ้วน (เช่น การกระจายแบบ Student’s t) และหางกุด (เช่น การกระจายแบบ Uniform)2
การกระจายที่มีหางอ้วน คือ การกระจายที่ฟังก์ชันการกระจาย เป็นไปตาม (ในกรณีหางด้านขวา) หรือ (ในกรณีหางด้านซ้าย) เมื่อ หรือกล่าวง่าย ๆ ว่า คือ การกระจายที่ส่วนหางของการกระจายลดลงด้วย power rate ซึ่งหาก (หรือเรียกว่า Tail Index) ยิ่งต่ำ ฟังก์ชันการกระจายยิ่งลดลงช้า ส่วนหางของการกระจายยิ่งอ้วน ซึ่งหมายถึงโอกาสในการเกิด Rare Events เช่น วิกฤตค่าเงิน ยิ่งสูง
การกระจายที่มีหางอ้วนต่างจากการกระจายที่มีหางบาง เช่น การกระจายแบบปกติ ตรงที่ส่วนหางของการกระจายแบบปกติลดลงตาม exponential rate () ซึ่งเร็วกว่า power rate หางของการกระจายแบบปกติจึงแบนกว่า ดังนั้น EVT จึงถูกนำมาใช้ในการศึกษาลักษณะการกระจายในส่วนหางของตัวแปร ซึ่งคือการศึกษาความน่าจะเป็นของการเกิด Rare Events ของตัวแปรนั้น ๆ โดยการประมาณค่า Tail Index
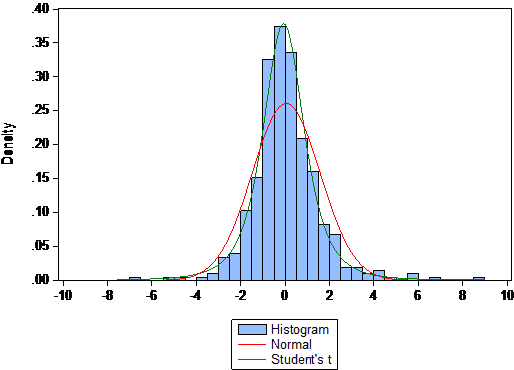
รูปที่ 1 แสดงการกระจายของดัชนี EMP จากข้อมูลของไทยในเดือนมกราคม ปี พ.ศ.2517 ถึงเดือนธันวาคม ปี พ.ศ.2554 โดยด้านขวาของการกระจาย แสดงถึงแรงกดดันต่อค่าเงินบาทในขาลง คือเมื่ออุปทานของเงินบาทสูงกว่าอุปสงค์ต่อเงินบาท ส่วนด้านซ้ายของการกระจาย แสดงถึงแรงกดดันต่อค่าเงินบาทในขาขึ้น ซึ่งเมื่อพิจารณา histogram แท่งสีฟ้า พบว่าการกระจายของดัชนี EMP มีลักษณะค่อนข้างสมมาตรแต่ leptokurtic คือเป็นการกระจายที่มีลักษณะโด่งในช่วงกลางของข้อมูลและมีหางของการกระจายที่อ้วน
การกระจายของดัชนี EMP ในรูปที่ 1 แสดงให้เห็นว่าดัชนี EMP มีการกระจายที่ต่างจากการกระจายแบบปกติ เพราะเมื่อเปรียบเทียบการกระจายแบบปกติซึ่งแสดงโดยเส้นสีแดงกับการกระจายแบบ Student’s t ซึ่งแสดงโดยเส้นสีเขียว พบว่าการกระจายแบบ Student’s t สอดคล้องกับข้อมูลมากกว่า สามารถอธิบายลักษณะโด่งในช่วงกลางและส่วนหางที่อ้วนได้ดีกว่า
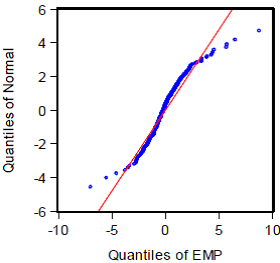
การกระจายในส่วนหางของดัชนี EMP ต่างจากการกระจายแบบปกติอย่างชัดเจนเมื่อพิจารณา Panel A ในรูปที่ 2 ซึ่งแสดง q-q plot ของดัชนี EMP เทียบกับกรณีที่ดัชนี EMP มีการกระจายแบบปกติ จุดสีน้ำเงินซึ่งมีลักษณะเป็นรูปตัว S เบ้ขวา ปลายด้านขวาลากยาวกว่าปลายด้านซ้าย แสดงว่าโอกาสที่จะเกิดวิกฤตค่าเงินบาทขาลงมีสูงกว่าโอกาสที่จะเกิดวิกฤตค่าเงินบาทขาขึ้น
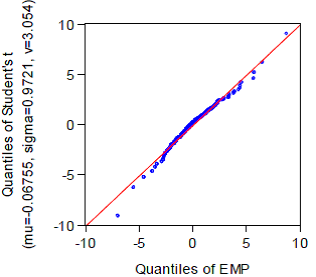
เมื่อพิจารณา Panel B ในรูปที่ 2 ซึ่งแสดงกรณีที่ดัชนี EMP มีการกระจายแบบ Student’s t พบว่าจุดสีน้ำเงินเรียงอยู่บนเส้นสีแดงได้ดีกว่าใน Panel A มาก โดยเฉพาะอย่างยิ่งในส่วนกลางของการกระจาย รูปที่ 2 สอดคล้องกับรูปที่ 1 ที่แสดงให้เห็นว่าการกระจายของดัชนี EMP มีลักษณะการกระจายคล้ายการกระจายแบบ Student’s t มากกว่าการกระจายแบบปกติ
หางที่อ้วนของการกระจายแบบ Student’s t แสดงให้เห็นว่าหากนำการกระจายแบบปกติมาประเมินความน่าจะเป็นของวิกฤตค่าเงินบาท ณ ระดับเดียวกัน ความน่าจะเป็นที่ประเมินได้จะต่ำเกินจริง แต่หากประเมินความน่าจะเป็นของวิกฤตค่าเงินโดยใช้ Student’s t ตาม Panel B ความน่าจะเป็นของวิกฤตค่าเงินบาทขาขึ้น (หางด้านซ้ายของการกระจาย) จะสูงเกินจริง ขณะที่ความน่าจะเป็นของวิกฤตค่าเงินบาทขาลง (หางด้านขวาของการกระจาย) ) จะยังต่ำเกินจริง
EVT จึงเป็นทางเลือกหนึ่งในการประเมินความน่าจะเป็นของการเกิด Rare Events โดยที่ไม่ต้องกำหนดรูปแบบของการกระจาย และยังสามารถใช้ประเมินความน่าจะเป็นในกรณีที่การกระจายไม่สมมาตร คือ ความอ้วนของหางทั้งสองข้างไม่เท่ากันได้อีกด้วย
นอกจากนั้นความสัมพันธ์ระหว่างตัวแปรในส่วนหางของการกระจาย (Tail Dependence) ยังอาจแตกต่างไปจากความสัมพันธ์ในช่วงกลางของการกระจาย ดังนั้นเมื่อใช้ EVT แบ่งการกระจายออกเป็นส่วนกลางและส่วนหางแล้ว เพื่อศึกษาว่าการเคลื่อนไหวที่ผิดปกติ ซึ่งหมายถึงการเคลื่อนไหวในส่วนหางของปัจจัยทางเศรษฐศาสตร์ สามารถใช้เป็นตัวพยากรณ์การเกิดวิกฤตค่าเงินได้หรือไม่ บทความนี้ได้ทำการทดสอบว่าดัชนี EMP และปัจจัยทางเศรษฐศาสตร์ มีความสัมพันธ์แบบ Asymptotic Dependence หรือไม่
ดัชนี EMP และปัจจัยทางเศรษฐศาสตร์ มีความสัมพันธ์กันในลักษณะ Asymptotic Dependence เมื่อ กล่าวคือหากปัจจัยทางเศรษฐศาสตร์ มีการเคลื่อนไหวขนาดใหญ่มาก ๆ () มีความน่าจะเป็นที่จะเกิดวิกฤตค่าเงิน หรือโอกาสที่ดัชนี EMP จะมีขนาดใหญ่มาก ๆ เช่นกัน แต่หากตัวแปรทั้งสองไม่มีความสัมพันธ์กันในลักษณะ Asymptotic Dependence โอกาสที่จะเกิดวิกฤตค่าเงินจะเท่ากับศูนย์ ปัจจัยทางเศรษฐศาสตร์ตัวนั้นจึงไม่เหมาะที่จะใช้เป็นตัวพยากรณ์การเกิดวิกฤต เพราะขณะที่ปัจจัยทางเศรษฐศาสตร์ มีขนาดใหญ่ขึ้นโอกาสการเกิดวิกฤตค่าเงินจะลดลงและเท่ากับศูนย์ในที่สุด
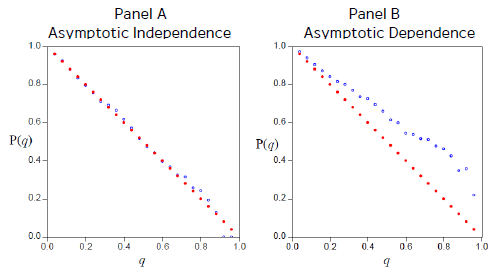
รูปที่ 3 แสดงให้เห็นความแตกต่างระหว่างตัวแปรที่มีความสัมพันธ์แบบ Asymptotic Independence (Panel A) และแบบ Asymptotic Dependence (Panel B) ในกรณีที่ตัวแปรมีความสัมพันธ์แบบ Asymptotic Independence ยิ่งตัวแปรทางเศรษฐศาสตร์มีขนาดใหญ่ เคลื่อนไหวลึกเข้าไปในส่วนหางของการกระจาย (คือ เมื่อความน่าจะเป็น ที่แสดงบนแกนนอนเข้าใกล้ 1) ความน่าจะเป็นที่จะเกิดวิกฤตขนาดใหญ่จะยิ่งลดลงและเข้าใกล้ศูนย์ แต่หากตัวแปรมีความสัมพันธ์แบบ Asymptotic Dependence เช่นใน Panel B ความน่าจะเป็นดังกล่าวจะเข้าใกล้ค่าคงที่ค่าหนึ่งที่มากกว่าศูนย์ ตัวแปรนั้น ๆ จึงสามารถพยากรณ์โอกาสการเกิดวิกฤตค่าเงินได้ โดยแสดงความน่าจะเป็นของการเกิดวิกฤตเมื่อปัจจัยทางเศรษฐศาสตร์เคลื่อนไหวผิดปกติ
เมื่อนำข้อมูลของไทยช่วงเดือนมกราคม ปี พ.ศ.2517 ถึงเดือนธันวาคม ปี พ.ศ.2554 มาใช้ในการประมาณค่า Tail Index โดยใช้ Hill (1975) estimator ร่วมกับการทำ Simulation ตามงานของ Jansen and de Vries (1991) พบว่า ไม่ใช่แต่เฉพาะดัชนี EMP ที่มีการกระจายแบบหางอ้วน ตัวแปรทางเศรษฐศาสตร์ของไทยที่นำมาศึกษาทั้งสิ้น 21 ตัวแปร เกือบทั้งหมดมีการกระจายแบบหางอ้วน ดังนั้นการกระจายแบบปกติจึงไม่เหมาะสมที่จะนำมาใช้ในการศึกษาความน่าจะเป็นของตัวแปรเหล่านี้ โดยเฉพาะในส่วนหางของการกระจาย เพราะอาจทำให้ความน่าจะเป็นที่ประมาณการณ์ได้ต่ำเกินจริง
เมื่อพิจารณาข้อมูลรายเดือนของดัชนี EMP พบว่าตั้งแต่ประเทศไทยใช้ระบบอัตราแลกเปลี่ยนลอยตัวแบบมีการจัดการ โอกาสการเกิดวิกฤตเงินบาทแข็งค่าอยู่ที่ประมาณ 5.6% (หนึ่งเดือนในทุก ๆ ปีครึ่ง) สูงกว่าโอกาสของการเกิดวิกฤตเงินบาทอ่อนค่าซึ่งอยู่ที่ 2.5% (หนึ่งเดือนในทุก ๆ 40 เดือน) แต่เมื่อหาปัจจัยทางเศรษฐศาสตร์ที่จะสามารถพยากรณ์หรือส่งสัญญาณเตือนการเกิดวิกฤตค่าเงินเหล่านี้โดยการทดสอบหาความสัมพันธ์แบบ Asymptotic Dependence ระหว่างดัชนี EMP กับปัจจัยทางเศรษฐศาสตร์ในช่วง 1–12 เดือนก่อนหน้าตามวิธีของ Poon, Rockinger and Tawn (2004) กลับแทบไม่พบความสัมพันธ์
อย่างไรก็ตาม ผลการศึกษาแสดงว่ามีตัวแปร 3 ตัวที่สามารถนำมาใช้พยากรณ์การเกิดวิกฤตค่าเงินได้ กล่าวคือ หากในเดือนก่อนหน้ามีการลดลงของทุนสำรองระหว่างประเทศหรือการเพิ่มขึ้นของปริมาณเงิน (เทียบกับทุนสำรองระหว่างประเทศ) อย่างผิดปกติ คือ เกินกว่า 9.9% และ 3.4% ตามลำดับโอกาสการเกิดวิกฤตเงินบาทอ่อนค่าของเดือนนี้จะสูงกว่า 40% ส่วนทางด้านการแข็งค่าของเงินบาทพบว่า วิกฤตอาจเกิดขึ้นในเดือนปัจจุบันด้วยความน่าจะเป็นเกิน 30% หากประมาณครึ่งปีก่อนหน้านี้อัตราดอกเบี้ยของไทยเพิ่มสูงกว่าอัตราดอกเบี้ยของสหรัฐฯ เกิน 0.24% ส่วนปัจจัยทางเศรษฐศาสตร์อื่น ๆ ที่ไม่พบความสัมพันธ์กับดัชนี EMP ปัจจัยเหล่านั้นไม่เหมาะที่จะนำมาใช้เป็นตัวพยากรณ์หรือตัวส่งสัญญาณการเกิดวิกฤตค่าเงิน
นอกจากนั้นผลการศึกษายังแสดงว่า EVT สามารถเลือกตัวส่งสัญญาณการเกิดวิกฤตค่าเงินได้ดีกว่าแบบจำลอง Probit เพราะปัจจัยทางเศรษฐศาสตร์ที่เลือกตามวิธีของ EVT มีความสามารถในการพยากรณ์สูงกว่า ดังนั้นโดยสรุปแล้ว อาจกล่าวได้ว่า EVT เป็นเครื่องมือหนึ่งที่น่าจะนำมาใช้ในการศึกษาการเกิดวิกฤตค่าเงินและหาปัจจัยทางเศรษฐศาสตร์ที่สามารถส่งสัญญาณเตือนการเกิดวิกฤตค่าเงิน เนื่องจาก EVT เป็นการศึกษาเฉพาะส่วนหางของการกระจาย ซึ่งความสัมพันธ์ระหว่างตัวแปรในส่วนหางและช่วงกลางของการกระจายอาจมีความแตกต่างกัน และ EVT ยังสามารถทดสอบความสัมพันธ์ Asymptotic Dependence ระหว่างตัวแปร ซึ่งเป็นคุณลักษณะสำคัญของตัวส่งสัญญาณการเกิดวิกฤต
Cumperayot, P. (2015), ‘ Stability of Thai Baht: Tales from the Tails ’, Bulletin of Economic Research, Forthcoming.
Eichengreen, B., Rose, A.K. and Wyplosz, C. (1996), ‘Exchange Market Mayhem: The Antecedents and Aftermath of Speculative Attacks’, Economic Policy, 21, pp. 249–312.
Hill, B. (1975), ‘A Simple General Approach to Inference about the Tail of a Distribution’, Annals of Mathematical Statistics, 3, pp. 1163–74.
International Monetary Fund (2008), ‘How the IMF Promotes Global Economic Stability’, A Factsheet-April 2008.
Jansen, D.W. and de Vries, C.G. (1991), ‘On the Frequency of Large Stock Returns, Putting Boom and Busts into Perspective’, Review of Economics and Statistics, 73, pp. 18–24.
Poon, S., Rockinger, M. and Tawn, J. (2004), ‘Extreme-Value Dependence in Financial Markets: Diagnostics, Models and Financial Implications’, Review of Financial Studies, 17, pp. 581–610.
ข้อคิดเห็นที่ปรากฏในบทความนี้เป็นความเห็นของผู้เขียน ซึ่งไม่จำเป็นต้องสอดคล้องกับความเห็นของสถาบันวิจัยเศรษฐกิจป๋วย อึ๊งภากรณ์