ดัชนี MPI ไม่สะท้อน GDP ภาคอุตสาหกรรมจริงหรือ?

excerpt
ดัชนีผลผลิตอุตสาหกรรมหรือ Manufacturing Production Index (MPI) คือดัชนีรายเดือนที่ถูกสร้างขึ้นเป็นข้อมูลเร็วเพื่อช่วยสะท้อน GDP ภาคอุตสาหกรรมซึ่งเป็นข้อมูลเศรษฐกิจรายไตรมาสที่สำคัญของประเทศ ที่ผ่านมาดัชนี MPI สะท้อน GDP ภาคอุตสาหกรรมได้ดีมากระดับหนึ่ง แต่ทว่าภายหลังวิกฤตอุทกภัยปี 2011 ผู้ใช้ข้อมูล (ทั้งผู้วิเคราะห์และผู้วางนโยบาย) เริ่มมองว่าดัชนี MPI ไม่สามารถบ่งชี้ GDP ภาคอุตสาหกรรมได้ดังเดิมซึ่งอาจเกิดจากการเปลี่ยนแปลงโครงสร้างการผลิตของประเทศ บทความนี้ต้องการแสดงให้เห็นว่า ความสัมพันธ์ของดัชนี MPI และ GDP ภาคอุตสาหกรรมอาจมีความผิดปกติได้ในบางช่วงเวลา ทั้ง ๆ ที่ไม่มีการเปลี่ยนแปลงใด ๆ ในเชิงโครงสร้างการผลิตหรือปัจจัยพื้นฐานที่เชื่อมโยงความสัมพันธ์ระหว่างดัชนี MPI และ GDP ภาคอุตสาหกรรม หากแต่เป็นผลมาจากวิธีที่ดัชนี MPI และ GDP ภาคอุตสาหกรรมถูกสร้างขึ้น นี่คือข้อเท็จจริงที่ผู้ใช้ข้อมูลควรตระหนักถึง การเลือกใช้หรือปรับใช้เครื่องมือทางเศรษฐมิติให้เหมาะสมสำหรับการวิเคราะห์ข้อมูลเพื่อติดตามภาวะเศรษฐกิจของประเทศจึงเป็นสิ่งจำเป็น
“I am too familiar with the manner in which actual data are met with the suggestion that the other data, if they were collected, might show something else to believe it to have any value as an argument. “Statistics on the table, please” can be my sole reply.”
— Karl Pearson, 1910
การติดตามภาวะเศรษฐกิจเป็นสิ่งสำคัญสำหรับทุกภาคส่วนของระบบเศรษฐกิจ ผู้ดำเนินนโยบายจำเป็นต้องติดตามภาวะเศรษฐกิจเพื่อปรับนโยบายให้เหมาะสมต่อการเติบโตอย่างมีเสถียรภาพของประเทศ ความเข้าใจในภาวะเศรษฐกิจสามารถช่วยให้ภาคธุรกิจและภาคครัวเรือนตัดสินใจเรื่องการลงทุน การบริโภค หรือการออมได้อย่างมีประสิทธิภาพภายใต้ความไม่แน่นอนของวัฏจักรเศรษฐกิจ สำหรับประเทศไทยนั้นภาคอุตสาหกรรมถือได้ว่ามีความสำคัญต่อเศรษฐกิจของประเทศ โดยข้อมูลที่เป็นทางการของภาวะเศรษฐกิจภาคอุตสาหกรรมนั้นดูได้จากตัวเลขผลิตภัณฑ์มวลรวมประชาติ (GDP) ภาคอุตสาหกรรม อย่างไรก็ดี ความถี่รายไตรมาสของข้อมูล GDP ภาคอุตสาหกรรมนั้นอาจจะช้าเกินไปสำหรับการติดตามภาวะเศรษฐกิจ สำนักงานเศรษฐกิจอุตสาหกรรม กระทรวงอุตสาหกรรม จึงพัฒนาดัชนีผลผลิตอุตสาหกรรมหรือ Manufacturing Production Index (MPI) ขึ้นมาเพื่อเป็นข้อมูลเร็ว (มีความถี่ของการเผยแพร่รายเดือน) ที่สามารถสะท้อน GDP ภาคอุตสาหกรรมได้ ซึ่งที่ผ่านมาดัชนีดังกล่าวมีประโยชน์ต่อการติดตามภาวะกิจกรรมภาคอุตสาหกรรมของประเทศอย่างมาก แต่ทว่าภายหลังวิกฤตน้ำท่วมในปี 2011 ดัชนี MPI ถูกมองว่าให้ภาพที่ผิดเพี้ยนไปและควรมีการทบทวนวิธีจัดเก็บดัชนีดังกล่าว บทความนี้จะวิเคราะห์ว่าแนวคิดดังกล่าวมีความน่าเชื่อถือมากน้อยเพียงใด
MPI เป็นดัชนีที่ถูกสร้างมาเพื่อสะท้อนการผลิตภาคอุตสาหกรรมของไทย โดยสำนักงานเศรษฐกิจอุตสาหกรรมทำการสุ่มสำรวจภาคเอกชนเพื่อวัดระดับการผลิตภาคอุตสาหกรรมของไทยในแต่ละเดือน ในขณะที่ตัวเลข GDP ภาคอุตสาหกรรมก็ถูกสร้างจากการสุ่มสำรวจระดับการผลิตภาคอุตสาหกรรมเช่นกัน แต่กลุ่มสำรวจของการคำนวณตัวเลข GDP จะใหญ่กว่ากลุ่มสำรวจของดัชนี MPI หากจะมองแบบง่าย ๆ ก็คือ กลุ่มสำรวจของ MPI เป็น subset ของกลุ่มสำรวจของ GDP ภาคอุตสาหกรรม เพราะฉะนั้นตามหลักการและวิธีการจัดเก็บข้อมูลดัชนี MPI น่าจะสามารถสะท้อน GDP ภาคอุตสาหกรรมได้ดีระดับหนึ่ง
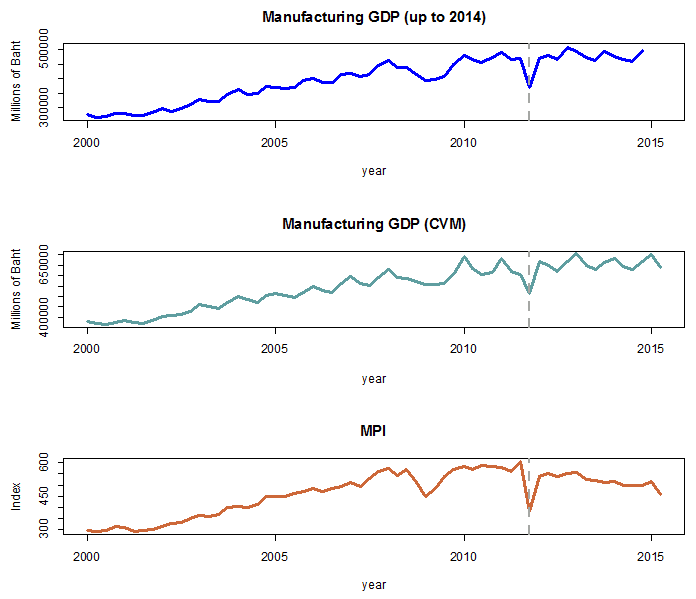
ภาพที่ 1 แสดงทิศทางข้อมูลรายไตรมาสตั้งแต่ไตรมาสที่ 1 ปี 2000 ถึง ไตรมาส 2 ปี 2015 ของ GDP ภาคอุตสาหกรรมที่คำนวณโดยใช้ Fixed-weighted Index (ซึ่งมีข้อมูลถึงปี 2014) และ Chained Volume Measures (CVM) และดัชนี MPI ที่ถูกแปลงเป็นดัชนีรายไตรมาส โดยเส้นประแสดงช่วงเวลาที่เกิดมหาอุทกภัย ภาพที่ 1 แสดงให้เห็นว่า
- ดัชนี MPI สะท้อนแนวโน้มระยะยาว (long-run dynamics) ของ GDP ภาคอุตสาหกรรมได้ดีมาก โดยค่า R-squared ที่ได้จากการใช้ Regression Analysis เพื่อศึกษา Linear relationship ของ (Natural Logarithm) ดัชนี MPI และ (Natural Logarithm) GDP ภาคอุตสาหกรรมมีค่าสูงถึง 0.93 และ 0.88 สำหรับ GDP แบบ Fixed-weighted Index และ CVM ตามลำดับ
- โดยรวมแล้วหากไม่นับความผันผวนด้านฤดูกาล (Seasonal Variation) ดัชนี MPI มีความผันผวนสูงกว่า GDP ภาคอุตสาหกรรม โดยสังเกตได้ชัดในช่วงวิกฤตเศรษฐกิจโลกปี 2009 และวิกฤตน้ำท่วมปี 2011
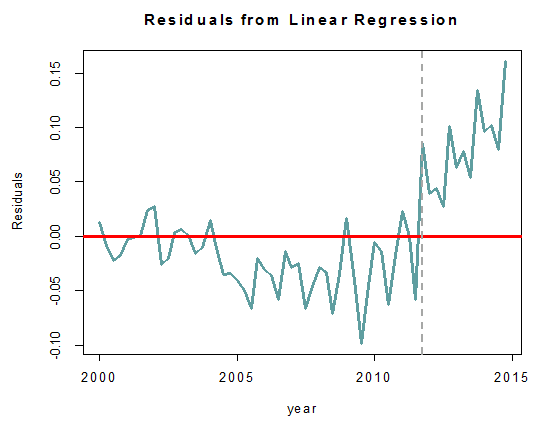
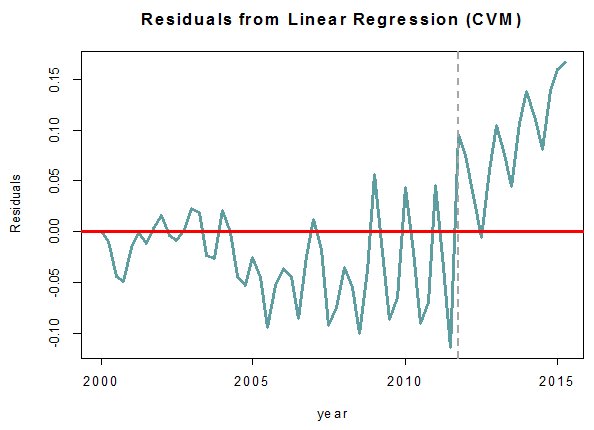
อย่างไรก็ดี หากพิจารณา Residuals ที่ได้จาก Regression Analysis ที่ใช้ศึกษา Linear Relationship ของ (Natural Logarithm) ดัชนี MPI และ (Natural Logarithm) GDP ภาคอุตสาหกรรมทั้งแบบ Fixed-weighted Index และ CVM ดังที่แสดงในภาพที่ 2 และ 3 ตามลำดับ จะเห็นว่าภายหลังวิกฤตน้ำท่วมปี 2011 (เส้นประ) เริ่มมีความผิดปกติเกิดขึ้น หากดัชนี MPI สะท้อน GDP ภาคอุตสาหกรรมในระยะสั้น (Short-run Dynamics) ได้ดี Residuals ควรจะเคลื่อนไหวขึ้นลงที่ระดับค่าศูนย์ (เส้นแดง) แต่ทว่าภายหลังวิกฤตน้ำท่วมค่า Residuals ที่ได้มีค่าเป็นบวกและมีแนวโน้มสูงขึ้นอย่างต่อเนื่อง ข้อเท็จจริงนี้อาจส่งผลให้ผู้ใช้ข้อมูลรู้สึกว่าวิกฤตน้ำท่วมอาจเป็นปัจจัยที่ก่อให้เกิดการเปลี่ยนแปลงเชิงโครงสร้าง (Structural Change) ของอุตสาหกรรมไทย โดยมีเหตุผลในเชิงธุรกิจที่เกิดขึ้นภายหลังวิกฤตน้ำท่วมมาสนับสนุนแนวความคิดดังกล่าวด้วย
อันที่จริงการที่ดัชนี MPI สะท้อน GDP ภาคอุตสาหกรรมได้ไม่ดีในบางช่วงเวลานั้นไม่ใช่เรื่องผิดปกติ เราสามารถอธิบายพฤติกรรมดังกล่าวได้โดยใช้ความรู้จากวิชาสถิติเบื้องต้น หลักการ Law of Large Numbers ชี้ให้เห็นว่า (ภายใต้สมมติฐานทั่วไป) ค่าเฉลี่ยของ Random Variables จะผันผวนน้อยลงเมื่อขนาดของ Sample Size ใหญ่ขึ้น จากที่ได้นำเสนอไปแล้วข้างต้นว่ากลุ่มสำรวจของ MPI เป็น Subset ของกลุ่มสำรวจของ GDP ภาคอุตสาหกรรม โดยดัชนี MPI และ GDP ภาคอุตสาหกรรมถือได้ว่าเป็น Weighted Averages ของข้อมูลจากกลุ่มสำรวจ เนื่องจากกลุ่มสำรวจของ GDP ภาคอุตสาหกรรมมีขนาดใหญ่กว่าจึงมีความผันผวนน้อยกว่าความผันผวนของดัชนี MPI (ซึ่งข้อสรุปนี้สอดคล้องกับพฤติกรรมของ MPI และ GDP ภาคอุตสาหกรรมที่แสดงในภาพที่ 1) โดยข้อสรุปที่ได้นี้สามารถทำความเข้าใจได้โดยใช้เลขคณิตอย่างง่าย เช่น หากกลุ่มสำรวจมีขนาดเล็ก ค่าเฉลี่ย Weighted Average อาจได้รับอิทธิพลจาก Extreme Values หรือ Outliers ได้มากกว่ากลุ่มสำรวจที่มีขนาดที่ใหญ่กว่า หากธุรกิจบางประเภทที่อยู่ในกลุ่มสำรวจมีผลประกอบการที่ดีมาก ก็อาจจะทำให้ดัชนี MPI มีค่าที่สูงกว่าเมื่อเทียบกับ GDP ภาคอุตสาหกรรมซึ่งมีกลุ่มสำรวจที่ใหญ่กว่าและตัวหารที่มากกว่า
นอกจากนี้ ข้อมูลเศรษฐกิจที่เป็น Time Series ในแต่ละช่วงเวลาจะมีความสัมพันธ์กัน (Time Dependence) ยกตัวอย่างเช่น ข้อมูล GDP ที่สะท้อนวัฏจักรเศรษฐกิจ (Business Cycles) จะแสดงให้เห็นถึงช่วงเวลาที่เศรษฐกิจดีหรืออยู่ในช่วงขาขึ้น (Boom) และช่วงเวลาที่เศรษฐกิจแย่หรือในช่วงขาลง (Bust) และมีความหนืด (Persistence) ของการเคลื่อนไหว เช่น ช่วงเศรษฐกิจทั้งขาขึ้นและขาลงโดยเฉลี่ยแล้วจะกินเวลาหลายปี และเช่นเดียวกันสำหรับข้อมูลผลประกอบการของภาคธุรกิจ แต่ละบริษัทก็จะมีช่วงขาขึ้นและขาลงที่กินเวลายาวนานระดับหนึ่ง
เมื่อนำปัจจัยทั้งเรื่องของ Law of Large Numbers และ Persistence ของข้อมูลเศรษฐกิจมาวิเคราะห์พร้อมกันก็จะสามารถอธิบายความผิดปกติของดัชนี MPI เมื่อเทียบกับ GDP ภาคอุตสาหกรรมได้ เช่น หากภาคธุรกิจบางกลุ่มที่อยู่ในกลุ่มสำรวจของ MPI อยู่ในช่วงขาขึ้น ด้วยขนาดกลุ่มสำรวจที่เล็กกว่า ดัชนี MPI อาจจะมีค่าที่สูงกว่าที่ควรจะเป็นเมื่อเทียบกับ GDP ภาคอุตสาหกรรม และด้วย Persistence ของข้อมูลก็อาจส่งผลให้ดัชนี MPI มีค่าที่สูงกว่าที่ควรจะเป็นเมื่อเทียบกับ GDP ภาคอุตสาหกรรมเป็นระยะเวลานานระดับหนึ่ง
เพื่อให้ผู้อ่านเข้าใจเหตุผลทางเศรษฐมิติที่เสนอมาข้างต้น เราจึงขอนำเสนอ Monte Carlo Simulation ที่จะสะท้อนความสัมพันธ์ระหว่างดัชนี MPI และ GDP ภาคอุตสาหกรรม เนื่องจากดัชนี MPI และ GDP ภาคอุตสาหกรรมมีคุณสมบัติแบบ Nonstationary ที่มี Unit Root และการศึกษา Time Series ที่มีคุณสมบัติดังกล่าวจะซับซ้อน เพื่อความเรียบง่ายเราจึงขอนำเสนอการทำ Monte Carlo Simulation เลียนแบบพฤติกรรมของดัชนี MPI และ GDP ภาคอุตสาหกรรม ภายใต้สมมติฐานที่ว่าข้อมูลทั้งสองมีคุณสมบัติ Stationary โดยสมมติฐานนี้จะไม่กระทบต่อข้อสรุปสำคัญที่เราต้องการนำเสนอ สำหรับการทำ Simulation นั้น เราสร้างข้อมูลเสมือนด้านการผลิตของ 400 บริษัทในภาคอุตสาหกรรม ภายใต้สมมติฐานที่ว่าการผลิตของแต่ละบริษัทมีลักษณะเป็น Stationary ที่เคลื่อนไหวขึ้นลงอยู่ในระดับศูนย์ (Means are equal to zero)
สำหรับการทำ Simulation นั้นเราใช้ package arima.sim ใน R เพื่อสร้างข้อมูลเสมือนด้านการผลิตของ 400 บริษัทในภาคอุตสาหกรรม เพื่อความสะดวกในการทำ Simulation เราสร้างข้อมูลเสมือนภายใต้สมมติฐานที่ว่า (1) การผลิตของทั้ง 400 บริษัทนั้นไม่มีความสัมพันธ์กัน (Independence) และ (2) การผลิตของแต่ละบริษัทสอดคล้องกับ Autoregressive Process of Order 1 หรือ AR(1) โดยมี Autoregressive Parameter เท่ากับ 0.95 และ Seed ที่ใช้ในการ Simulate ข้อมูลคือ 12345 โดยความยาวของข้อมูลอยู่ที่ 150 ไตรมาส
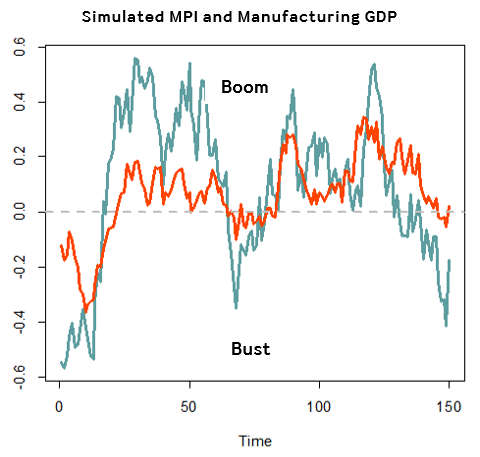
เมื่อได้ข้อมูลเสมือนด้านการผลิตของ 400 บริษัทแล้ว เราใช้สมมติฐานที่ว่า 100 บริษัทแรกอยู่ในกลุ่มตัวอย่างของ MPI และ 400 บริษัททั้งหมดอยู่ในกลุ่มตัวอย่าง GDP ภาคอุตสาหกรรม เพื่อให้ดัชนี MPI และ GDP ภาคอุตสาหกรรมมีหน่วย (Scale) เดียวกันซึ่งจะเอื้อต่อการเปรียบเทียบเชิงลึก เราใช้การทำ Normalization และการคำนวณดัชนี MPI และ GDP ภาคอุตสาหกรรมแบบง่าย โดยคำนวณค่าเสมือนของดัชนี MPI จากค่าเฉลี่ยของการผลิตของ 100 บริษัทแรก และคำนวณ GDP ภาคอุตสาหกรรมจากค่าเฉลี่ยของการผลิตของทั้ง 400 บริษัท โดยภาพที่ 4 แสดงค่าเสมือนของดัชนี MPI (เส้นสีฟ้า) และ ค่าเสมือนของ GDP ภาคอุตสาหกรรม (เส้นสีส้ม)
จากภาพที่ 4 จะสังเกตได้ว่า (1) ค่าเสมือนของดัชนี MPI มีความผันผวนมากกว่าค่าเสมือนของ GDP ภาคอุตสาหกรรม ซึ่งสามารถอธิบายได้จาก Law of Large Numbers (2) ค่าเสมือนทั้งสองมีความ Persistence โดยจะเคลื่อนไหวอยู่ที่ค่ากลางที่ศูนย์ ส่วนค่าที่มากกว่าศูนย์อาจจะแปลได้ว่าเป็นขาขึ้นของเศรษฐกิจ ในขณะที่ค่าที่ต่ำกว่าศูนย์อาจจะแปลได้ว่าเป็นขาลงของเศรษฐกิจ (3) จะสังเกตได้ว่าในช่วงไตรมาสที่ 1 ถึงประมาณไตรมาสที่ 20 ค่าเสมือนของดัชนี MPI มีค่าที่ต่ำกว่าค่าเสมือนของ GDP ภาคอุตสาหกรรม และหลังจากนั้นก็กลับมีค่าที่สูงกว่าจนถึงในช่วงไตรมาสที่ 60 และลักษณะดังกล่าวก็เริ่มเปลี่ยนทิศทางอีกครั้ง โดยข้อสังเกตนี้สอดคล้องกับการนำ Law of Large Numbers มาประยุกต์ใช้กับความ Persistence ดังที่อธิบายไว้ข้างต้น คือในช่วงเศรษฐกิจขาลง MPI มีแนวโน้มต่ำกว่า GDP ภาคอุตสาหกรรม และในทางกลับกันสำหรับช่วงเศรษฐกิจขาขึ้น MPI มีแนวโน้มสู่งกว่า GDP ภาคอุตสาหกรรม
โดยข้อสังเกตสุดท้ายนี้สอดคล้องกับทิศทางการเคลื่อนไหวของดัชนี MPI และ GDP ภาคอุตสาหกรรมในภาพที่ 2 และ 3 หากพิจารณาจาก Residuals จากผล Regression Analysis แล้วจะเห็นได้ว่า โดยรวมแล้วในช่วงปี 2000–2011 นั้นค่าของ Residuals มีค่าเป็นลบ ซึ่งสะท้อนว่า GDP ภาคอุตสาหกรรมมีค่าต่ำกว่าค่าที่ดัชนี MPI คาดการณ์ไว้ ซึ่งหมายความว่าดัชนี MPI มีค่าสูงเมื่อเทียบกับ GDP ภาคอุตสาหกรรม โดยสอดคล้องกับเศรษฐกิจที่อยู่ในช่วงขาขึ้น และภายหลังปี 2011 ค่าของ Residuals มีค่าเป็นบวก ซึ่งสะท้อนว่าดัชนี MPI มีค่าต่ำเมื่อเทียบกับ GDP ภาคอุตสาหกรรม โดยสอดคล้องกับขาลงของภาคอุตสาหกรรมภายหลังวิกฤตน้ำท่วมจนถึงปัจจุบัน
กล่าวโดยสรุปคือหลักการ Law of Large Numbers และ Persistence สามารถใช้อธิบายความผิดปกติ (Anomaly) จากความสัมพันธ์ของดัชนี MPI และ GDP ภาคอุตสาหกรรมที่ผู้ใช้ข้อมูลกังวลได้ ซึ่งความปกติที่ดูเสมือนเป็นความผิดปกติดังกล่าวเกิดจากวิธีการที่ดัชนี MPI และ GDP ภาคอุตสาหกรรมถูกสร้างขึ้นมา และอาจไม่เกี่ยวกับการเปลี่ยนแปลงทางโครงสร้างการผลิตครั้งใหญ่ภายหลังวิกฤตน้ำท่วมปี 2011
วิธีการวิเคราะห์ข้อมูลทั่วไปของผู้ใช้ข้อมูลอาจส่งผลให้ดัชนี MPI ดูผิดเพี้ยนไปมากกว่าเดิม โดยเฉพาะอย่างยิ่งจาก (1) การใช้ข้อมูลทางเศรษฐกิจที่ผ่านการขจัดปัจจัยทางฤดูกาล (Deseasonalized Time Series) และ (2) วิธีการขจัดปัจจัยด้านฤดูกาลที่ผู้ใช้ข้อมูลในประเทศไทยนิยมใช้ในปัจจุบัน โดยเราขออ้างอิงความเห็นของ V. Gomez และ A. Maravall ผู้ที่ผลักดันการขจัดปัจจัยด้านฤดูกาลที่ได้รับความนิยมทั่วโลก ใน Gomez, V., Maravall A. (2001) ที่ว่า
“data used in econometric models should not be, as a rule, seasonally adjusted”
Thawornkaiwong (2016) ได้อธิบายไว้ว่าทำไม V. Gomez และ A. Maravall จึงมีความคิดเช่นนี้และทำไมวิธีการขจัดฤดูกาลของไทยจึงมีปัญหา ผู้อ่านสามารถอ่านเพิ่มเติมได้จาก Ghysels et al. (1996) ในอีกหลายปัญหาที่เกิดจากการขจัดปัจจัยด้านฤดูกาล
บทความนี้ได้นำเสนออีกแง่มุมในการวิเคราะห์พฤติกรรมของดัชนี MPI ที่มักถูกมองว่ามีความผิดปกติในสายตาของผู้ใช้ข้อมูล เราได้แสดงให้เห็นว่าหลักการเบื้องต้นของวิชาสถิติและเศรษฐมิติสามารถอธิบายพฤติกรรมที่เสมือนผิดปกตินี้ได้ และเราได้แสดงให้เห็นว่าพฤติกรรมที่เสมือนผิดปกติจริง ๆ แล้วคือความปกติที่เราจะเห็นจากความสัมพันธ์ของดัชนี MPI และ GDP ภาคอุตสาหกรรม โดยนัยเชิงนโยบายที่ได้จากบทความนี้คือ ผู้ใช้ข้อมูลควรปรับปรุงวิธีการวิเคราะห์ข้อมูลดังกล่าวโดยมีสามทางเลือกหลัก ๆ คือ
ใช้เครื่องมือวิเคราะห์ที่ใช้ประโยชน์จากความหนืดและความสัมพันธ์เชิงโครงสร้างของแต่ละภาคอุตสาหกรรม (Spatio-temporal Dependence) ในข้อมูลเศรษฐกิจ เนื่องจากแต่ละบริษัทในภาคธุรกิจเดียวกันน่าจะมีการผลิตที่คล้ายคลึงกันอันเป็นผลจาก Business Cycles ของแต่ละภาคธุรกิจ ดังนั้นเราสามารถใช้ข้อมูลของบริษัทที่อยู่ในกลุ่มสำรวจ MPI เพื่อประมาณการการผลิตของบริษัทที่ไม่ได้อยู่ในกลุ่มสำรวจของ MPI โดยวิธีนี้จะทำให้กลุ่มสำรวจของดัชนี MPI เสมือนว่าใหญ่ขึ้นซึ่งจะช่วยแก้ไขปัญหาของขนาดกลุ่มสำรวจที่เล็กของดัชนี MPI ได้ในทางอ้อม
เนื่องจากดัชนี MPI สามารถอธิบาย Long-run Dynamics ของ GDP ภาคอุตสาหกรรมได้ดีมาก ในขณะที่ไม่สามารถอธิบาย Short-run Dynamics ได้ดีสักเท่าไหร่ ผู้ใช้ข้อมูลจะต้องพยายามเลือกใช้เครื่องมือทางเศรษฐมิติที่เหมาะสมเพื่อปรับปรุง Short-run Dynamics ของแบบจำลองซึ่งเครื่องมือเหล่านี้ได้ถูกพัฒนามากว่า 40 ปีแล้ว
อันที่จริงการใช้ดัชนี MPI เพื่อติดตามภาวะเศรษฐกิจนั้นจุดมุ่งหมายหลักคือการดูแนวโน้มของเศรษฐกิจ ความสำคัญของข้อมูลต่าง ๆ คือความสามารถในการสะท้อนแนวโน้มเศรษฐกิจของประเทศ ผู้ใช้ข้อมูลสามารถหลีกเลี่ยงปัญหาที่อาจเกิดขึ้นจากการขจัดปัจจัยทางฤดูกาลและหลีกเลี่ยงปัญหาจากความไม่สมบูรณ์ในการอธิบาย Short-run Dynamics ของแบบจำลองได้โดยใช้ Linear Filters ที่เหมาะสมในการหาแนวโน้ม (Trend) ของเศรษฐกิจซึ่งได้ถูกนำเสนอใน Thawornkaiwong (2016)
ท้ายสุดนี้ผู้เขียนเห็นร่วมกับ Karl Pearson ว่าความพยายามพัฒนาข้อมูลให้มีความถูกต้องแม่นยำเป็นสิ่งที่น่าชื่นชม อย่างไรก็ดีความเข้าใจเครื่องมือทางสถิติที่ใช้ การวิเคราะห์ข้อมูลอย่างถูกวิธีและรอบด้านก็มีความสำคัญเช่นกัน Statistics on the table, please.
กิตติกรรมประกาศ
ผู้เขียนขอขอบคุณ คุณวรวิทย์ มโนปิยอนันต์ สำหรับข้อมูลดัชนี MPI และ GDP ภาคอุตสาหกรรม คุณอโนทัย พุทธารี ดร. เสาวณี จันทะพงษ์ คุณณัชพล จรูญพิพัฒน์กุล และคุณวรดา ลิ้มเจริญรัตน์ สำหรับคำแนะนำต่าง ๆ ที่ช่วยให้บทความนี้สมบูรณ์ขึ้น
Ghysels, E., C.W.J. Granger and P. Siklos (1996): “Is seasonal adjustment a linear or nonlinear data filtering process?” Journal of Business and Economic Statistics 14, 374–386.
Gomez, V. and A. Maravall (2001): “Seasonal adjustment and signal extraction in economic time series.” In Pena, D., G.C. Tiao and R.S. Tsay (Eds.), A Course in Time Series Analysis, J. Wiley and Sons, New York.
Thawornkaiwong, S. (2016); “Simplified spectral analysis for exploratory data analysis of Economic Time Series.” Forthcoming PIER Discussion Paper.